RSA(一) 背后的数学原理

前言

本篇文章将试图从数学原理上理清 RSA 的加密解密的原理；并写一个简单的加密解密的用例来使用；

备注，本文是作者的原创作品，转载请注明出处。

数论相关

模 N

随机选择两个大的质数 p 和 q，p 不等于 q, 计算得到 $N = pq$

欧拉函数的值 r = 𝜑(pq)

$$r = 𝜑(pq) = 𝜑(p)𝜑(q) = (p-1)(q-1)$$

欧拉函数值求的是有多少个小于 N 的数与 N 互质，如果 N 本身为质数，那么就有 N-1 个数与 N 互质；

随机数 e

选择一个整数 e 且 $1 < e < r$，使得 e 与 r 互质(两个数的公约数为 1)；取 e 的目的是为了求得 e 关于 r 的模反元素 d；

模反元素 d

什么是模反元素 d

由e小节可知，模反元素 d 是 e 关于 r 的模反元素且若模反元素 d 存在，当且仅当 e 与 r 互质；

模反元素的数学意义

$$ed\equiv 1\pmod r$$

若 e 与 r 互质，那么总会找到这么一个数 d，使得 ed 和 1 与模 r 同余；通俗的说法既是，ed 除以 r 的余数与 1 除以 r 的余数相等，因为 1 除以 r 的余数恒等于 1，所以 ed 除以 r 的余数为 1，也就推出

$$ed-1=kr$$

，该表达式的意思就是 ed - 1 是 r 的倍数；

如何计算得到 d

那么如何计算得出此模反元素 d 呢？

根据扩展欧几里得算法的公式有，在$\pmod r$之下，

$$ex + ry=1$$

，此时 x 的解既是 e 关于模 r 的一个模反元素；认真的读者读到这里，肯定会产生疑问，上面的公式 $ed-1=kr$ 怎么看起来与 $ex+ry=1$ 怎么这么像呢，但是又有差别，我们将公式 $ed-1=kr$ 调整一下，得到

$$ed-kr=1 … ①$$

将扩展欧几里得算法的公式 $ex + ry=1$ 的 x、y 值进行替换，x = d, y = k，得到

$$ed+kr=1 … ②$$

什么，两个看似如此矛盾的两个不同的方程(公式 ① 和公式 ②)… 什么意思？谁是对的？谁是错的？

摘抄模反元素中的一段内容如下，

事实上， $x+kn(k ∈ ℤ)$都是a关于模n的模逆元，这里我们取最小的正整数解 $x \pmod n (x < n)$

对应到我们的例子中来，也就是 $d+kr(k ∈ ℤ)$ 都是 e 关于模 r 的模逆元，这里我们取最小的正整数解 $d \pmod r (d < r)$；由此可知，d 的解实际上有无限多个，满足 $d+kr(k ∈ ℤ)$；k 是整数集合，包含正整数、负整数和零；

其实，公式①和公式②其实可以理解为同一个方程，只是 Y 轴（这里指 K 轴）的方向发生了变化而已；

加密和解密

假设 Bob 想给 Alice 送一个消息 m；

公钥和密钥

在 Alice 端，经过上述的步骤，我们总共得到了 6 个数字，p、q、N、r、e、d；并生成公钥和密钥，公钥就是$(N、e)$组合；秘钥就是$(N、d)$组合；并且 Alice 将公钥发送给 Bob；

加密过程

Bob 想给 Alice 送一个消息 M，他拥有 Alice 的公钥，既是 $(N、e)$ 。他使用起先与 Alice 约好的编码格式将 M 转换为一个小于 模 N，且与 N 互质的整数 m；通常，我们传递的是字符串，但是字符可以转换为对应的 ASCII 码值或者 UNICODE 等整数数值；由于转换后的数字必须要小于 N，所以，一般的做法是，将原来的文本切割为很多小份，然后分别加密，将每一段转换为 m 后再传输；

加密公式，

$$c\equiv m^{e} \pmod N$$

将 m 转换为加密数值c，然后 Bob 将c传输给 Alice；那么c是如何计算得到的？其实这个求c的过程非常的简单，直接是

$$c=m^e\%N$$

推导过程，$u=m^e\%N$，因为 $u < N$ 导出 $u=u\%N$ 导出 $c=u$ 导出 余数 u 既是c

https://l2x.gitbooks.io/understanding-cryptography/docs/chapter-3/rsa.html

解密过程

Alice 拿到 Bob 的加密信息c以后，她使用下面的公式来将c解密得到 m：

$$c^d\equiv m\pmod N$$

同加密过程求c一样，这里，得出 $$m=c^d\%N$$

这里的关键问题是，如何得到的解密方程式 $c^d\equiv m\pmod N$？

公式推导

由加密公式，

$$c\equiv m^e \pmod N$$

通过同余的基本运算规则

那么可以得出

$$c^d\equiv m^{ed} \pmod N$$

下面相关部分摘要自 wikipedia，稍有不同的是，上述过程的原始消息是 m，下面过程的原始消息是 n

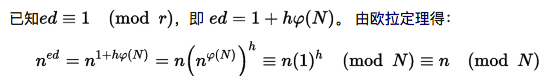
上面推论的重点在于，$n(n^{φ(N)})^h\equiv n(1)^h \pmod N$ 是怎么导出来的？参考欧拉定理

所以，有 $n^{φ(N)}\equiv 1\pmod N$，难道是将 $n^{φ(N)}\equiv 1\pmod N$ 直接代入 $n(n^{φ(N)})^h$，所以得到 $n(n^{φ(N)})^h\equiv n(1)^h \pmod N$，除此之外，想不到原因了… 但是在同余中没找到这种参数代入法.. 所以会有些怀疑；好吧，姑且给自己有一个悬念吧..

最终，经过上述的论证，我们得到了解密要用到的公式，

$$c^d\equiv m\pmod N$$

https://l2x.gitbooks.io/understanding-cryptography/docs/chapter-3/rsa.html

例证

上面的原理性的东西说了一堆，这里通过一个实际的例子来看看 RSA 是如何做到加密解密的？

Bob 试图通过 RSA 的加密的方式向 Alice 发送数据，

生成密钥

如下步骤描述了 Alice 如何通过 RSA 算法生成自己的密钥(公钥和公钥)；

1. 模 N，Alice 选择两个质数 5、13，得到
   $$N=5\times13=65$$
   备注，这里选择的时候一定要注意，之前就是因为错选了不是质数的 9，导致入坑很久没爬出来；

2. 欧拉函数值 r
   $$r=φ(N)=φ(5)φ(13)=(5-1)(13-1)=48$$

3. 随机数 e，随机选择 e 且 $(1 < e < r)$，e 必须与 r 互质，这里，我随机选择一个
   $$e=5$$

4. 求 e 关于 r 的模反元素 d，有公式 $ed\equiv 1\pmod r$ 等价于求解
   $$5 \times d \equiv 1\pmod {48}$$
   按照如何计算得到 d中所介绍的扩展欧几里得算法，得到公式
   $$5\times d + 48k=1$$，同样也可以按照公式$$5\times d - 48k=1$$来进行求解，两者之间的相互区别在如何计算得到 d有详细的描述；

   为了计算出 d，我按照求解的公式 $5\times d - 48k=1$ 写了一段程序来求解 d，从 k = -20 开始，不断的试探出 d 的取值，

   int k = -20;
   
   int e = 5;
   
   int r = 48;
   
   while( true ){
      
      int d_mod = (r*k + 1)%e;
   
      if( d_mod == 0 ){
         
         int d = ( (r*k + 1)/e );
         
         System.out.println("=====> k="+k+"; d=" + d );
                     
         //break;
         
      }
      
      //System.out.println("tried k="+k);       
      
      k ++;
      
      if( k > 10 ) break;
      
   }

   求得取值范围如下，

   =====> k=-17; d=-163
   =====> k=-12; d=-115
   =====> k=-7; d=-67
   =====> k=-2; d=-19
   =====> k=3; d=29
   =====> k=8; d=77

   这里要求取最小正整数的模反元素，所以取得 d = 29，k = 3；因为这里是按照$ed-kr=1$的逻辑进行求解，所以，这里 k 的值为正整数 3，如果是按照扩展欧几里得算法的方式$ed+kr=1$求解，那么 k = -3

Ok，至此，重要的 6 个元素已经集合完毕，他们分别是 $p=5, q=13, N=65, r=48, e=5, d=29$

于是，得到公钥为 ${65, 5}$；得到私钥为 ${65, 29}$；最后 Alice 通过某种方式将公钥发送给 Bob；

传输加密信息

Bob 通过 RSA 加密方式向 Alice 发送字符感叹号 !，

首先，将字符 ! 转换成其对应的 ASCII 码值，对应为 41，记为 $m$

再次，通过加密公式 $c=m^e\%N$ 既 $c=41^5\%65=6$，由此得到 m 的加密后的数字为 $c = 6$；注意，过程中使用到了 (N,e)；备注，这里可用编程的方式求解，

System.out.println( Math.pow(41,5) % 65);

最后，Bob 将加密数字 c = 6 发送给了 Alice；

解密加密信息

Alice 接收到了 Bob 发送的加密数字 c (6)，之后使用私钥(65, 29)进行解密，

首先，根据解密公式 $m=c^d\%N$ 既 $m=6^{29}\%65$，解出 $m=41$，正好得到 Bob 未加密之前的字符 ! 的 ASCII 码，因此，这里成功将其解密；备注，这里可以通过编程的方式求解，

System.out.println( Math.pow(6,29) % 65);

为什么 RSA 很难被破解

因为要通过密文 c 反推得到明文 m，根据解密方程式 $m=c^d\%N$ 我们知道，

1. 在公钥公开的前提下，既是知道 N、e 的前提下，必须要知道 d，才能解密出明文 m；
2. 而要知道 d，那么就必须对素数模 N 进行因式分解，得到 p 和 q，
3. 再通过欧拉函数的计算 $𝜑(pq)=𝜑(p)𝜑(q)$ 得到 r，
4. 最后通过 r 和 e，求出 e 于 r 的模反元素的计算才能最终推导出 d；

而一切的一切的前提都必须对 N 进行因式分解，而如果 N 是一个非常大的素数，因式分解几乎是不可能的；这样，也就保证了 RSA 的加密技术的可靠性；

使用注意

可以看到，在加密和解密过程中都会涉及到特大指数级别的运算，所以，运算过程是非常耗费计算机资源和时间的；所以一般的通讯中不直接使用 RSA 来进行加密通讯；而是通过公钥加密一段 DES 密钥来进行通讯，比如 Bob 使用 Alice 的公钥生成一个 DES 对称密钥，然后发送给 Alice，然后 Alice 再使用密钥解密得到 DES 密钥，这样双发最后实际上是通过 DES 密钥在进行通讯；

References

https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95

https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference

https://l2x.gitbooks.io/understanding-cryptography/docs/chapter-3/rsa.html